In the thrilling world of football, fans passionately argue over their favorite lineups, managers spend hours planning, and analysts pore over player statistics. Selecting the ideal combination of players to build an unbeatable squad requires balancing rigorous analysis with gut instinct. Traditionally, such decisions are based upon the instincts of experts and by those closely associated with the world of football. Out of this, with advanced data analytics and machine learning coming to the fore, this very approach in itself transformed into an evidence-based method for better decision making.
This tutorial will guide you to use machine learning to create the ultimate European football dream team—that is, using a dataset from the UEFA Champions League 2021/2022 season—entails outlining steps to data preparation, feature selection, and predictive model development. Ending with visualizing the optimal lineup.

Step 1: Data Preparation
In the first step is to prepare the data. We start by csv files from the datasets that contain statistics on attacking, defending, distribution, goals, and key stats of the players.
import pandas as pd
# Load datasets
attacking = pd.read_csv("attacking.csv")
defending = pd.read_csv("defending.csv")
attempts = pd.read_csv("attempts.csv")
distribution = pd.read_csv("distributon.csv")
goals = pd.read_csv("goals.csv")
key_stats = pd.read_csv("key_stats.csv")
# Merge datasets
data = attacking.merge(defending, on=['player_name', 'club', 'position'], how='inner', suffixes=('_att', '_def')) \
.merge(attempts, on=['player_name', 'club', 'position'], how='inner', suffixes=('', '_attempts')) \
.merge(distribution, on=['player_name', 'club', 'position'], how='inner') \
.merge(goals, on=['player_name', 'club', 'position'], how='inner', suffixes=('', '_goals')) \
.merge(key_stats, on=['player_name', 'club', 'position'], how='inner', suffixes=('', '_key'))
print(data.head())
In this step, We merged the files using the shared columns: player name, club, and position.
Step 2: Feature Selection and Normalization
Next, we select the relevant features we need for our model and then normalize the data using StandartScaler to ensure that all features have the same contribution to the model's predictions output.
from sklearn.preprocessing import StandardScaler
# Select relevant features
features = ['assists', 'corner_taken', 'offsides', 'dribbles', 'total_attempts', 'on_target', 'off_target',
'blocked', 'balls_recoverd', 'tackles', 't_won', 't_lost', 'clearance_attempted',
'passes_attempted', 'passes_completed', 'goals', 'headers', 'inside_area', 'penalties',
'minutes_played','match_played']
features_with_suffixes = [col for col in data.columns if any(col.startswith(f) for f in features)]
X = data[features_with_suffixes]
y = data['goals']
# Normalize the features
scaler = StandardScaler()
X = scaler.fit_transform(X)
The features we have chosen cover offensive contributions (assists, dribbles, goals), defensive actions (tackles, clearances, balls recovered), playmaking abilities (passes attempted, passes completed, touches), and overall activity on the field (minutes played, distance covered). This way, we make sure we cover a complete evaluation of each player's skills and impact.
Step 3: Building the Machine Learning Model
The next essential step is to build the neural network model to predict player performance based on the selected features. The model is trained to minimize the mean squared error. which is a common loss function for regression tasks
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
# Define the model
model = Sequential([
Dense(128, activation='relu', input_shape=(X.shape[1],)),
Dropout(0.2),
Dense(64, activation='relu'),
Dropout(0.2),
Dense(32, activation='relu'),
Dense(1, activation='linear') # Output layer for regression
])
# Compile the model
model.compile(optimizer='adam', loss='mean_squared_error', metrics=['mae'])
# Train the model
model.fit(X, y, epochs=200, batch_size=32, validation_split=0.2)
The model is using a large number of dropout layers, which randomly turn off neurons during training to prevent overfitting, and dense layers with ReLU activation, which enable the model to handle complex relations in data. In the last layer, a linear form of activation was employed to predict continuous variables like player performance. The Adam optimizer is then used to optimize efficiently and mean squared error loss is used to guarantee low prediction errors. To gain further understanding of this, we additionally monitor the mean absolute error. With a batch size of 32 and a validation split of 20%, we will train the model over 200 epochs, which offers a reasonable mix between generalization and fine-tuning.

Step 4: Generating and Evaluating Formations
To select the best formation, we move into creating multiple random formations and evaluate each one of them. The formation with the highest predicted performance is selected to be the first on the rank.
import random
import itertools
# Function to generate random formations
def generate_random_formations(players, num_forwards, num_midfielders, num_defenders, num_formations=1000):
forwards = [player for player in players if player['position'] == 'Forward']
midfielders = [player for player in players if player['position'] == 'Midfielder']
defenders = [player for player in players if player['position'] == 'Defender']
formations = []
for _ in range(num_formations):
formation = (
random.sample(forwards, num_forwards),
random.sample(midfielders, num_midfielders),
random.sample(defenders, num_defenders)
)
formations.append(formation)
return formations
# Function to evaluate formations
def evaluate_formations(formations, model):
best_formation = None
best_performance = -float('inf')
for formation in formations:
players = list(itertools.chain(*formation))
features = []
for player in players:
player_features = []
for feature in features_with_suffixes:
player_features.append(player.get(feature, 0))
features.append(player_features)
features = scaler.transform(features)
predicted_performance = model.predict(features).sum()
if predicted_performance > best_performance:
best_performance = predicted_performance
best_formation = formation
return best_formation, best_performance
# Define players list
players = data.to_dict('records')
# Generate and evaluate formations
formations = generate_random_formations(players, num_forwards=3, num_midfielders=4, num_defenders=3, num_formations=2000)
best_formation, best_performance = evaluate_formations(formations, model)
In this step, a number of random team formations are generated by selecting different player combinations: 3 forwards, 4 midfielders, and 3 defenders. This created a total of 2000 different formations. By using this kind of approach, one can screen through a large space of feasible configurations of teams. After generating new formations, we used the trained machine-learning model to predict each formation's overall in-game performance.
Step 5: Visualizing the Best Formation
Finally, we visualize the best formation by plotting the players on a football pitch and displaying their predicted contributions.
import matplotlib.pyplot as plt
import matplotlib.patches as patches
def draw_pitch(ax=None):
if ax is None:
fig, ax = plt.subplots(figsize=(10, 7))
# Pitch Outline & Centre Line
pitch_elements = [
([0, 0], [0, 90]), ([0, 130], [90, 90]), ([130, 130], [90, 0]),
([130, 0], [0, 0]), ([65, 65], [0, 90]), ([16.5, 16.5], [65, 25]),
([0, 16.5], [65, 65]), ([16.5, 0], [25, 25]), ([130, 113.5], [65, 65]),
([113.5, 113.5], [65, 25]), ([113.5, 130], [25, 25]), ([0, 5.5], [54, 54]),
([5.5, 5.5], [54, 36]), ([5.5, 0], [36, 36]), ([130, 124.5], [54, 54]),
([124.5, 124.5], [54, 36]), ([124.5, 130], [36, 36])
]
for line in pitch_elements:
plt.plot(line[0], line[1], color="black")
# Draw Circles
circles = [
plt.Circle((65, 45), 9.15, color="black", fill=False),
plt.Circle((65, 45), 0.8, color="black"),
plt.Circle((11, 45), 0.8, color="black"),
plt.Circle((119, 45), 0.8, color="black")
]
for circle in circles:
ax.add_patch(circle)
# Draw Arcs
arcs = [
patches.Arc((11, 45), height=18.3, width=18.3, angle=0, theta1=308, theta2=52, color="black"),
patches.Arc((119, 45), height=18.3, width=18.3, angle=0, theta1=128, theta2=232, color="black")
]
for arc in arcs:
ax.add_patch(arc)
plt.axis("off")
def plot_formation(formation):
fig, ax = plt.subplots(figsize=(10, 7))
draw_pitch(ax)
# Define positions
positions = {
'Forward': [(105, 22.5), (105, 45), (105, 67.5)],
'Midfielder': [(75, 15), (75, 35), (75, 55), (75, 75)],
'Defender': [(45, 15), (45, 35), (45, 55)],
'Goalkeeper': [(10, 45)]
}
# Plot players
for pos, players in zip(['Forward', 'Midfielder', 'Defender'], formation):
for player, (x, y) in zip(players, positions[pos]):
ax.text(x, y, player['player_name'], ha='center', va='center', fontsize=12, bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.5'))
plt.show()
plot_formation(best_formation)
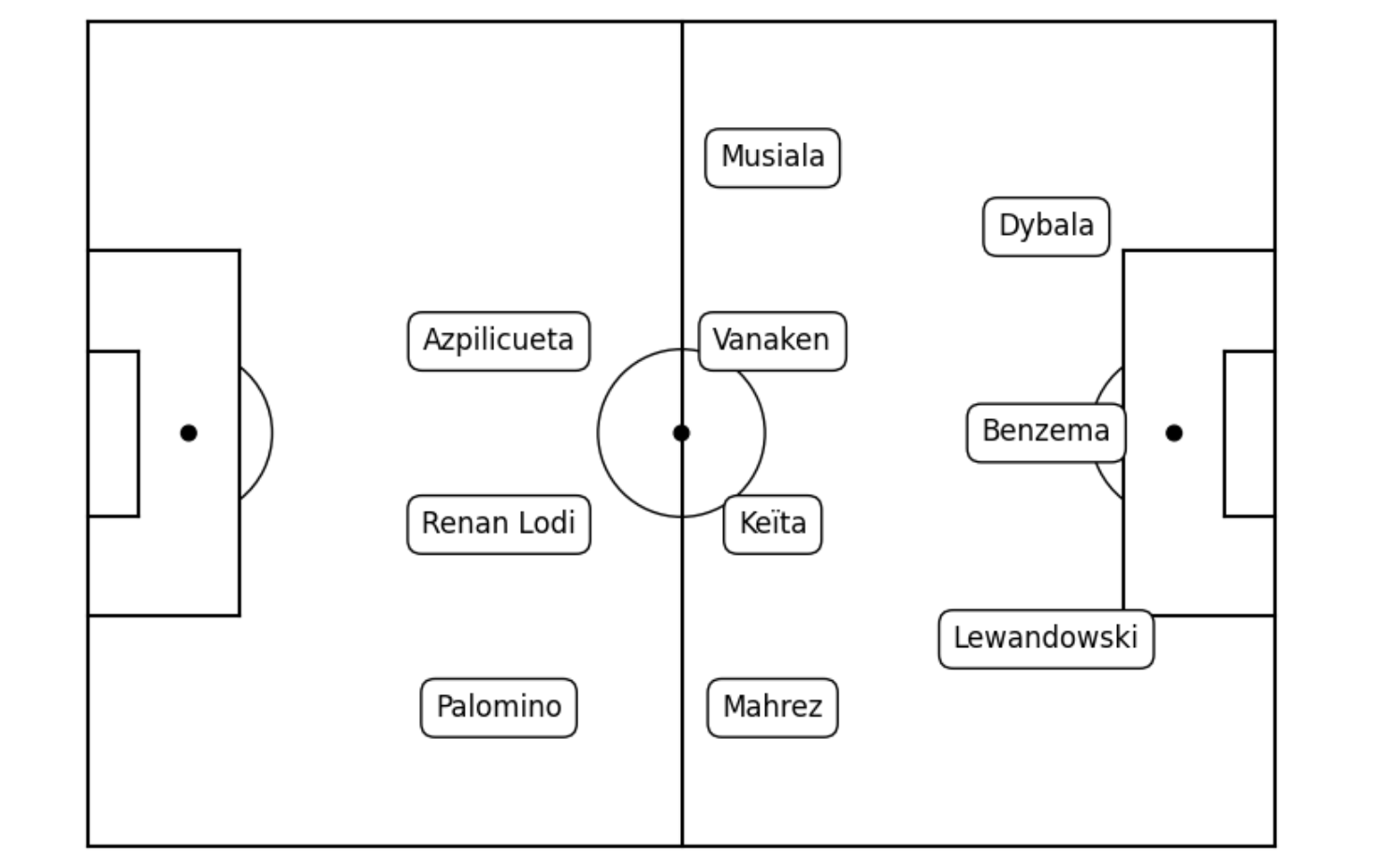
Conclusion
In this tutorial, we were able to use machine learning to present a football dream team that have the potential to be the best team with the best formation. The selection was based on statistical performance. However, our dataset was limited to the UEFA Champions League 2021/2022 season. I encourage you to experiment with different data sets, particularly the ones containing your local teams, in order to predict the ultimate lineup for your country. You may further improve the prediction accuracy and reliability of your results by using multiple machine learning models.
Larger datasets containing data from several years will enhance the value obtained from the analysis and provide better insight into player performance and team dynamics. Give it a shot and make sure to tell us about the results in the comments!

